Projection of Sphere Onto Xy Plane How to Draw
Vectors in Infinite
fourteen Cylindrical and Spherical Coordinates
Learning Objectives
- Catechumen from cylindrical to rectangular coordinates.
- Convert from rectangular to cylindrical coordinates.
- Convert from spherical to rectangular coordinates.
- Convert from rectangular to spherical coordinates.
The Cartesian coordinate system provides a straightforward way to draw the location of points in space. Some surfaces, still, can be difficult to model with equations based on the Cartesian system. This is a familiar problem; recall that in two dimensions, polar coordinates oft provide a useful alternative system for describing the location of a indicate in the plane, particularly in cases involving circles. In this section, we expect at two unlike ways of describing the location of points in space, both of them based on extensions of polar coordinates. As the name suggests, cylindrical coordinates are useful for dealing with problems involving cylinders, such equally calculating the volume of a round water tank or the amount of oil flowing through a pipe. Similarly, spherical coordinates are useful for dealing with bug involving spheres, such as finding the volume of domed structures.
Cylindrical Coordinates
When nosotros expanded the traditional Cartesian coordinate system from ii dimensions to three, we simply added a new axis to model the tertiary dimension. Starting with polar coordinates, nosotros can follow this same process to create a new iii-dimensional coordinate organisation, called the cylindrical coordinate organization. In this way, cylindrical coordinates provide a natural extension of polar coordinates to three dimensions.
Definition
In the cylindrical coordinate system, a point in space ((Figure)) is represented by the ordered triple ![]() where
where
The right triangle lies in the xy-plane. The length of the hypotenuse is ![]() and
and ![]() is the mensurate of the angle formed by the positive ten-axis and the hypotenuse. The
is the mensurate of the angle formed by the positive ten-axis and the hypotenuse. The
z-coordinate describes the location of the point higher up or beneath the xy-plane.
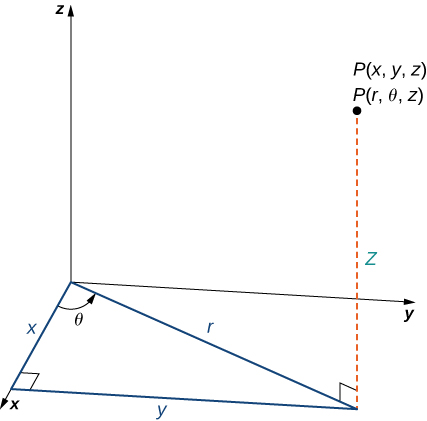
In the xy-plane, the correct triangle shown in (Figure) provides the key to transformation between cylindrical and Cartesian, or rectangular, coordinates.
Conversion between Cylindrical and Cartesian Coordinates
The rectangular coordinates ![]() and the cylindrical coordinates
and the cylindrical coordinates ![]() of a point are related as follows:
of a point are related as follows:

As when we discussed conversion from rectangular coordinates to polar coordinates in two dimensions, it should be noted that the equation ![]() has an infinite number of solutions. Yet, if we restrict
has an infinite number of solutions. Yet, if we restrict ![]() to values between
to values between ![]() and
and ![]() then we can find a unique solution based on the quadrant of the xy-plane in which original point
then we can find a unique solution based on the quadrant of the xy-plane in which original point ![]() is located. Note that if
is located. Note that if ![]() and so the value of
and so the value of ![]() is either
is either ![]() or
or ![]() depending on the value of
depending on the value of ![]()
Notice that these equations are derived from properties of right triangles. To make this like shooting fish in a barrel to see, consider point ![]() in the xy-plane with rectangular coordinates
in the xy-plane with rectangular coordinates ![]() and with cylindrical coordinates
and with cylindrical coordinates ![]() as shown in the following effigy.
as shown in the following effigy.
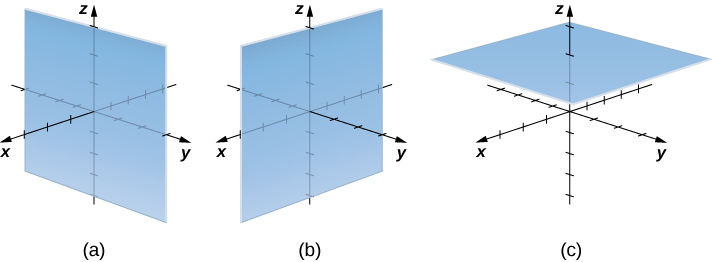
Permit'south consider the differences between rectangular and cylindrical coordinates past looking at the surfaces generated when each of the coordinates is held constant. If ![]() is a abiding, then in rectangular coordinates, surfaces of the form
is a abiding, then in rectangular coordinates, surfaces of the form ![]()
![]() or
or ![]() are all planes. Planes of these forms are parallel to the yz-airplane, the xz-plane, and the xy-plane, respectively. When we convert to cylindrical coordinates, the z-coordinate does not change. Therefore, in cylindrical coordinates, surfaces of the grade
are all planes. Planes of these forms are parallel to the yz-airplane, the xz-plane, and the xy-plane, respectively. When we convert to cylindrical coordinates, the z-coordinate does not change. Therefore, in cylindrical coordinates, surfaces of the grade ![]() are planes parallel to the xy-plane. Now, let'due south think about surfaces of the course
are planes parallel to the xy-plane. Now, let'due south think about surfaces of the course ![]() The points on these surfaces are at a fixed distance from the z-axis. In other words, these surfaces are vertical circular cylinders. Terminal, what about
The points on these surfaces are at a fixed distance from the z-axis. In other words, these surfaces are vertical circular cylinders. Terminal, what about ![]() The points on a surface of the form
The points on a surface of the form ![]() are at a fixed angle from the ten-centrality, which gives us a one-half-aeroplane that starts at the z-centrality ((Figure) and (Figure)).
are at a fixed angle from the ten-centrality, which gives us a one-half-aeroplane that starts at the z-centrality ((Figure) and (Figure)).
In rectangular coordinates, (a) surfaces of the form ![]() are planes parallel to the yz-aeroplane, (b) surfaces of the form
are planes parallel to the yz-aeroplane, (b) surfaces of the form ![]() are planes parallel to the xz-airplane, and (c) surfaces of the form
are planes parallel to the xz-airplane, and (c) surfaces of the form ![]() are planes parallel to the xy-aeroplane.
are planes parallel to the xy-aeroplane.
Converting from Cylindrical to Rectangular Coordinates
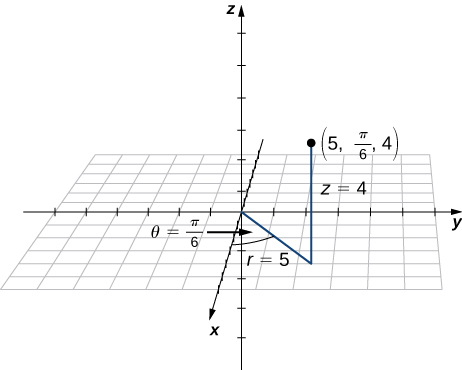
Plot the point with cylindrical coordinates ![]() and express its location in rectangular coordinates.
and express its location in rectangular coordinates.
Conversion from cylindrical to rectangular coordinates requires a simple application of the equations listed in (Effigy):
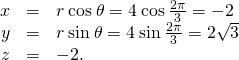
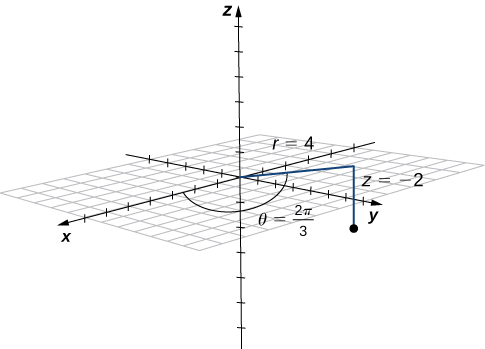
The point with cylindrical coordinates ![]() has rectangular coordinates
has rectangular coordinates ![]() (see the following figure).
(see the following figure).
The projection of the point in the xy-plane is 4 units from the origin. The line from the origin to the point's projection forms an angle of ![]() with the positive x-axis. The point lies
with the positive x-axis. The point lies ![]() units below the xy-airplane.
units below the xy-airplane.
Point ![]() has cylindrical coordinates
has cylindrical coordinates ![]() . Plot
. Plot ![]() and depict its location in space using rectangular, or Cartesian, coordinates.
and depict its location in space using rectangular, or Cartesian, coordinates.
The rectangular coordinates of the point are ![]()
Hint
The kickoff ii components match the polar coordinates of the point in the xy-plane.
If this procedure seems familiar, it is with good reason. This is exactly the aforementioned process that we followed in Introduction to Parametric Equations and Polar Coordinates to convert from polar coordinates to two-dimensional rectangular coordinates.
Converting from Rectangular to Cylindrical Coordinates
Convert the rectangular coordinates ![]() to cylindrical coordinates.
to cylindrical coordinates.
Use the second set of equations from (Figure) to translate from rectangular to cylindrical coordinates:
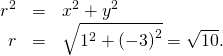
We choose the positive square root, so ![]() Now, we employ the formula to detect
Now, we employ the formula to detect ![]() In this case,
In this case, ![]() is negative and
is negative and ![]() is positive, which means we must select the value of
is positive, which means we must select the value of ![]() between
between ![]() and
and ![]()
![]()
In this instance, the z-coordinates are the aforementioned in both rectangular and cylindrical coordinates:
![]()
The indicate with rectangular coordinates ![]() has cylindrical coordinates approximately equal to
has cylindrical coordinates approximately equal to ![]()
Convert betoken ![]() from Cartesian coordinates to cylindrical coordinates.
from Cartesian coordinates to cylindrical coordinates.
![]()
Hint
![]() and
and ![]()
The utilise of cylindrical coordinates is common in fields such equally physics. Physicists studying electric charges and the capacitors used to store these charges have discovered that these systems sometimes have a cylindrical symmetry. These systems have complicated modeling equations in the Cartesian coordinate organisation, which brand them difficult to depict and analyze. The equations can often be expressed in more than elementary terms using cylindrical coordinates. For example, the cylinder described by equation ![]() in the Cartesian system can be represented past cylindrical equation
in the Cartesian system can be represented past cylindrical equation ![]()
Identifying Surfaces in the Cylindrical Coordinate Organization
Depict the surfaces with the given cylindrical equations.
Draw the surface with cylindrical equation ![]()
This surface is a cylinder with radius ![]()
Hint
The ![]() and
and ![]() components of points on the surface tin can take whatsoever value.
components of points on the surface tin can take whatsoever value.
Spherical Coordinates
In the Cartesian coordinate organisation, the location of a bespeak in space is described using an ordered triple in which each coordinate represents a altitude. In the cylindrical coordinate system, location of a point in infinite is described using ii distances ![]() and an bending measure
and an bending measure ![]() In the spherical coordinate organisation, we again utilise an ordered triple to describe the location of a point in space. In this case, the triple describes one distance and two angles. Spherical coordinates make it elementary to describe a sphere, but as cylindrical coordinates get in piece of cake to describe a cylinder. Grid lines for spherical coordinates are based on angle measures, similar those for polar coordinates.
In the spherical coordinate organisation, we again utilise an ordered triple to describe the location of a point in space. In this case, the triple describes one distance and two angles. Spherical coordinates make it elementary to describe a sphere, but as cylindrical coordinates get in piece of cake to describe a cylinder. Grid lines for spherical coordinates are based on angle measures, similar those for polar coordinates.
Definition
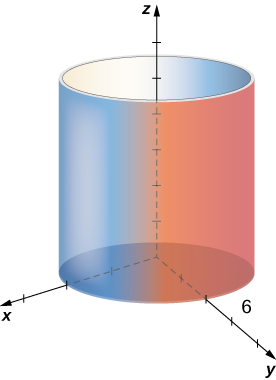
In the spherical coordinate system, a point ![]() in space ((Effigy)) is represented by the ordered triple
in space ((Effigy)) is represented by the ordered triple ![]() where
where
The relationship among spherical, rectangular, and cylindrical coordinates.
Past convention, the origin is represented as ![]() in spherical coordinates.
in spherical coordinates.
Converting among Spherical, Cylindrical, and Rectangular Coordinates
Rectangular coordinates ![]() and spherical coordinates
and spherical coordinates ![]() of a bespeak are related as follows:
of a bespeak are related as follows:
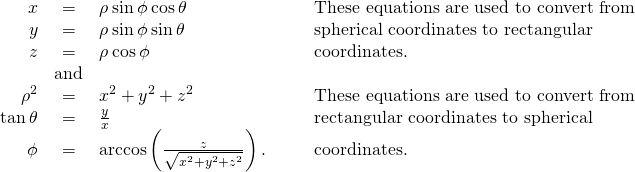
If a point has cylindrical coordinates ![]() then these equations define the relationship between cylindrical and spherical coordinates.
then these equations define the relationship between cylindrical and spherical coordinates.

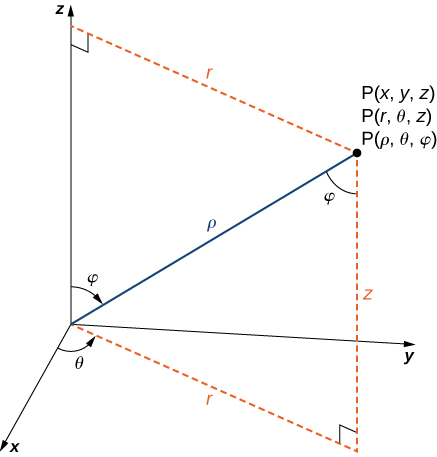
The formulas to catechumen from spherical coordinates to rectangular coordinates may seem circuitous, but they are straightforward applications of trigonometry. Looking at (Figure), it is easy to encounter that ![]() And so, looking at the triangle in the xy-airplane with
And so, looking at the triangle in the xy-airplane with ![]() as its hypotenuse, nosotros accept
as its hypotenuse, nosotros accept ![]() The derivation of the formula for
The derivation of the formula for ![]() is similar. (Figure) also shows that
is similar. (Figure) also shows that ![]() and
and ![]() Solving this terminal equation for
Solving this terminal equation for ![]() and so substituting
and so substituting ![]() (from the outset equation) yields
(from the outset equation) yields ![]() Also, note that, equally before, we must exist careful when using the formula
Also, note that, equally before, we must exist careful when using the formula ![]() to choose the right value of
to choose the right value of ![]()
The equations that convert from one system to another are derived from right-triangle relationships.
As we did with cylindrical coordinates, let's consider the surfaces that are generated when each of the coordinates is held constant. Allow ![]() be a constant, and consider surfaces of the form
be a constant, and consider surfaces of the form ![]() Points on these surfaces are at a fixed distance from the origin and form a sphere. The coordinate
Points on these surfaces are at a fixed distance from the origin and form a sphere. The coordinate ![]() in the spherical coordinate system is the same equally in the cylindrical coordinate system, and so surfaces of the form
in the spherical coordinate system is the same equally in the cylindrical coordinate system, and so surfaces of the form ![]() are one-half-planes, every bit before. Last, consider surfaces of the course
are one-half-planes, every bit before. Last, consider surfaces of the course ![]() The points on these surfaces are at a stock-still angle from the z-axis and form a half-cone ((Figure)).
The points on these surfaces are at a stock-still angle from the z-axis and form a half-cone ((Figure)).
Converting from Spherical Coordinates
Plot the point with spherical coordinates ![]() and express its location in both rectangular and cylindrical coordinates.
and express its location in both rectangular and cylindrical coordinates.
Use the equations in (Figure) to translate betwixt spherical and cylindrical coordinates ((Figure)):
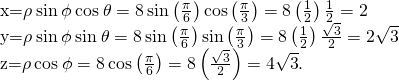
The project of the point in the xy-plane is ![]() units from the origin. The line from the origin to the point'southward projection forms an angle of
units from the origin. The line from the origin to the point'southward projection forms an angle of ![]() with the positive ten-centrality. The point lies
with the positive ten-centrality. The point lies ![]() units above the xy-plane.
units above the xy-plane.
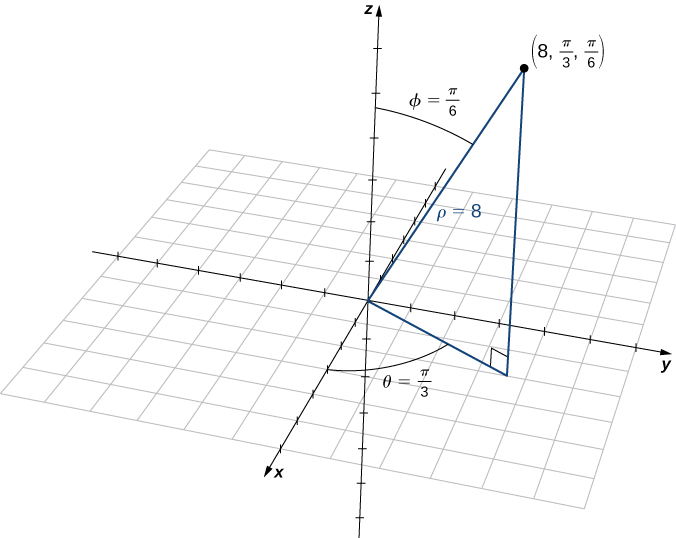
The betoken with spherical coordinates ![]() has rectangular coordinates
has rectangular coordinates ![]()
Finding the values in cylindrical coordinates is as straightforward:
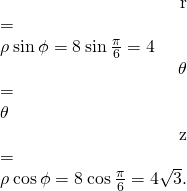
Thus, cylindrical coordinates for the bespeak are ![]()
Plot the point with spherical coordinates ![]() and draw its location in both rectangular and cylindrical coordinates.
and draw its location in both rectangular and cylindrical coordinates.
Hint
Converting the coordinates first may help to find the location of the betoken in space more easily.
Converting from Rectangular Coordinates
Convert the rectangular coordinates ![]() to both spherical and cylindrical coordinates.
to both spherical and cylindrical coordinates.
Start by converting from rectangular to spherical coordinates:
![]()
Considering ![]() and then the correct selection for
and then the correct selection for ![]() is
is ![]()
In that location are actually two ways to identify ![]() We tin can utilize the equation
We tin can utilize the equation ![]() A more simple approach, however, is to use equation
A more simple approach, however, is to use equation ![]() Nosotros know that
Nosotros know that ![]() and
and ![]() and so
and so
![]()
and therefore ![]() The spherical coordinates of the indicate are
The spherical coordinates of the indicate are ![]()
To notice the cylindrical coordinates for the point, we need only detect ![]()
![]()
The cylindrical coordinates for the point are ![]()
Identifying Surfaces in the Spherical Coordinate Arrangement
Describe the surfaces with the given spherical equations.
a. This is the fix of all points ![]() units from the origin. This fix forms a sphere with radius
units from the origin. This fix forms a sphere with radius ![]() b. This set of points forms a half plane. The bending between the half plane and the positive ten-axis is
b. This set of points forms a half plane. The bending between the half plane and the positive ten-axis is ![]() c. Permit
c. Permit ![]() exist a point on this surface. The position vector of this betoken forms an angle of
exist a point on this surface. The position vector of this betoken forms an angle of ![]() with the positive z-axis, which ways that points closer to the origin are closer to the centrality. These points form a half-cone.
with the positive z-axis, which ways that points closer to the origin are closer to the centrality. These points form a half-cone.
Hint
Think about what each component represents and what it means to hold that component constant.
Spherical coordinates are useful in analyzing systems that accept some degree of symmetry about a point, such equally the volume of the infinite inside a domed stadium or wind speeds in a planet's atmosphere. A sphere that has Cartesian equation ![]() has the simple equation
has the simple equation ![]() in spherical coordinates.
in spherical coordinates.
In geography, breadth and longitude are used to describe locations on Earth's surface, as shown in (Figure). Although the shape of Earth is non a perfect sphere, we use spherical coordinates to communicate the locations of points on Earth. Let's assume World has the shape of a sphere with radius ![]() mi. We express angle measures in degrees rather than radians because breadth and longitude are measured in degrees.
mi. We express angle measures in degrees rather than radians because breadth and longitude are measured in degrees.
In the latitude–longitude system, angles draw the location of a point on Earth relative to the equator and the prime number elevation.
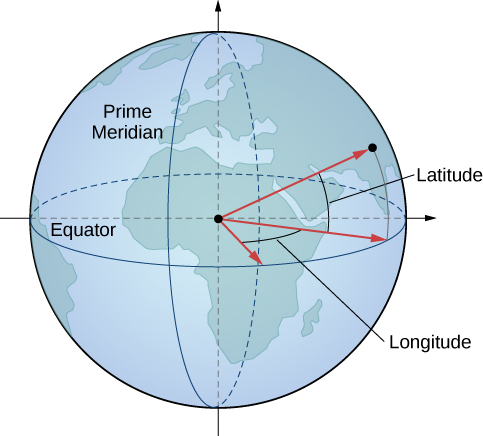
Let the center of Globe be the center of the sphere, with the ray from the center through the North Pole representing the positive z-centrality. The prime number meridian represents the trace of the surface as it intersects the xz-plane. The equator is the trace of the sphere intersecting the xy-airplane.
Sydney, Australia is at ![]() and
and ![]() Limited Sydney'south location in spherical coordinates.
Limited Sydney'south location in spherical coordinates.
![]()
Hint
Considering Sydney lies due south of the equator, nosotros demand to add together ![]() to find the bending measured from the positive z-centrality.
to find the bending measured from the positive z-centrality.
Cylindrical and spherical coordinates give us the flexibility to select a coordinate system advisable to the problem at hand. A thoughtful choice of coordinate system can make a trouble much easier to solve, whereas a poor option can lead to unnecessarily complex calculations. In the post-obit instance, nosotros examine several different problems and talk over how to select the best coordinate arrangement for each one.
Choosing the Best Coordinate System
In each of the following situations, nosotros decide which coordinate system is most appropriate and describe how we would orient the coordinate axes. There could be more one right answer for how the axes should exist oriented, but we select an orientation that makes sense in the context of the problem. Note: There is not enough data to set upwards or solve these problems; nosotros simply select the coordinate organisation ((Figure)).
- Observe the center of gravity of a bowling ball.
- Determine the velocity of a submarine subjected to an ocean electric current.
- Calculate the pressure in a conical water tank.
- Find the volume of oil flowing through a pipeline.
- Determine the amount of leather required to make a football game.
(credit: (a) modification of piece of work by scl hua, Wikimedia, (b) modification of piece of work by DVIDSHUB, Flickr, (c) modification of work by Michael Malak, Wikimedia, (d) modification of work by Sean Mack, Wikimedia, (e) modification of work by Elvert Barnes, Flickr)

- Clearly, a bowling brawl is a sphere, so spherical coordinates would probably work all-time hither. The origin should exist located at the physical center of the ball. There is no obvious option for how the ten-, y– and z-axes should be oriented. Bowling balls normally take a weight block in the center. I possible choice is to marshal the z-axis with the axis of symmetry of the weight cake.
- A submarine generally moves in a direct line. There is no rotational or spherical symmetry that applies in this situation, then rectangular coordinates are a skillful choice. The z-axis should probably point up. The ten– and y-axes could be aligned to indicate east and n, respectively. The origin should be some convenient concrete location, such every bit the starting position of the submarine or the location of a particular port.
- A cone has several kinds of symmetry. In cylindrical coordinates, a cone can be represented by equation
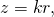 where
where 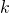 is a constant. In spherical coordinates, we accept seen that surfaces of the form
is a constant. In spherical coordinates, we accept seen that surfaces of the form 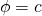 are half-cones. Last, in rectangular coordinates, elliptic cones are quadric surfaces and can be represented by equations of the grade
are half-cones. Last, in rectangular coordinates, elliptic cones are quadric surfaces and can be represented by equations of the grade 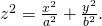 In this case, we could choose whatever of the three. Nevertheless, the equation for the surface is more complicated in rectangular coordinates than in the other two systems, so nosotros might want to avoid that choice. In addition, we are talking about a water tank, and the depth of the water might come into play at some indicate in our calculations, so it might exist nice to have a component that represents height and depth straight. Based on this reasoning, cylindrical coordinates might be the best choice. Cull the z-centrality to align with the axis of the cone. The orientation of the other 2 axes is arbitrary. The origin should exist the bottom bespeak of the cone.
In this case, we could choose whatever of the three. Nevertheless, the equation for the surface is more complicated in rectangular coordinates than in the other two systems, so nosotros might want to avoid that choice. In addition, we are talking about a water tank, and the depth of the water might come into play at some indicate in our calculations, so it might exist nice to have a component that represents height and depth straight. Based on this reasoning, cylindrical coordinates might be the best choice. Cull the z-centrality to align with the axis of the cone. The orientation of the other 2 axes is arbitrary. The origin should exist the bottom bespeak of the cone. - A pipeline is a cylinder, and so cylindrical coordinates would be best the all-time choice. In this case, however, we would likely cull to orient our z-centrality with the centre axis of the pipeline. The ten-axis could exist chosen to bespeak straight downward or to some other logical management. The origin should exist chosen based on the trouble statement. Notation that this puts the z-axis in a horizontal orientation, which is a little different from what we normally practice. It may make sense to choose an unusual orientation for the axes if information technology makes sense for the problem.
- A football has rotational symmetry near a primal axis, so cylindrical coordinates would piece of work best. The z-axis should align with the axis of the ball. The origin could exist the center of the ball or perhaps one of the ends. The position of the 10-axis is arbitrary.
Which coordinate organisation is most advisable for creating a star map, as viewed from Earth (see the post-obit figure)?
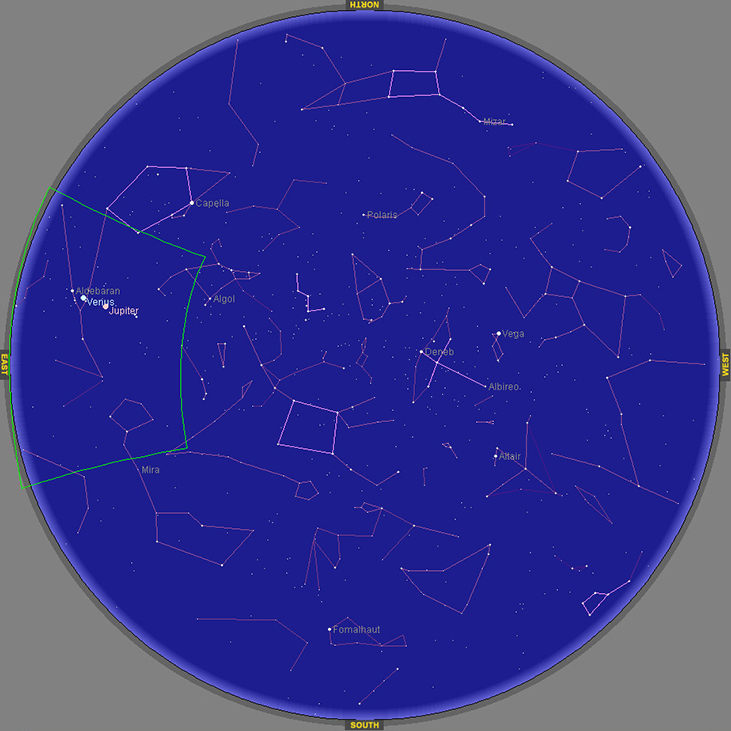
How should we orient the coordinate axes?
Spherical coordinates with the origin located at the center of the earth, the z-axis aligned with the Due north Pole, and the ten-axis aligned with the prime number elevation
Hint
What kinds of symmetry are present in this situation?
Primal Concepts
Use the post-obit figure every bit an aid in identifying the human relationship between the rectangular, cylindrical, and spherical coordinate systems.
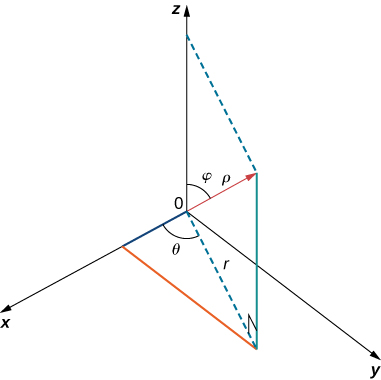
For the following exercises, the cylindrical coordinates ![]() of a betoken are given. Find the rectangular coordinates
of a betoken are given. Find the rectangular coordinates ![]() of the point.
of the point.
![]()
![]()
![]()
![]()
![]()
![]()
For the following exercises, the rectangular coordinates ![]() of a indicate are given. Detect the cylindrical coordinates
of a indicate are given. Detect the cylindrical coordinates ![]() of the betoken.
of the betoken.
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, the equation of a surface in cylindrical coordinates is given.
Observe the equation of the surface in rectangular coordinates. Identify and graph the surface.
[T] ![]()
A cylinder of equation ![]() with its middle at the origin and rulings parallel to the z-axis,
with its middle at the origin and rulings parallel to the z-axis,
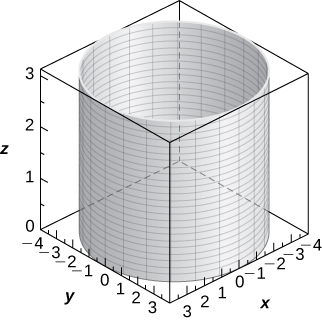
[T] ![]()
[T] ![]()
Hyperboloid of two sheets of equation ![]() with the y-axis as the axis of symmetry,
with the y-axis as the axis of symmetry,
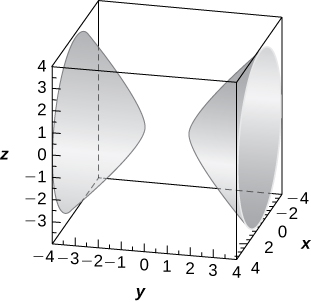
[T] ![]()
[T] ![]()
Cylinder of equation ![]() with a middle at
with a middle at ![]() and radius
and radius ![]() with rulings parallel to the z-axis,
with rulings parallel to the z-axis,
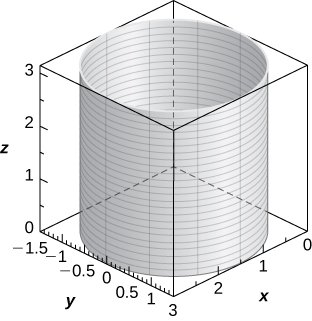
[T] ![]()
[T] ![]()
For the following exercises, the equation of a surface in rectangular coordinates is given. Notice the equation of the surface in cylindrical coordinates.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, the spherical coordinates ![]() of a point are given. Observe the rectangular coordinates
of a point are given. Observe the rectangular coordinates ![]() of the point.
of the point.
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, the rectangular coordinates ![]() of a point are given. Detect the spherical coordinates
of a point are given. Detect the spherical coordinates ![]() of the signal. Express the measure of the angles in degrees rounded to the nearest integer.
of the signal. Express the measure of the angles in degrees rounded to the nearest integer.
![]()
![]()
![]()
![]()
![]()
![]()
For the post-obit exercises, the equation of a surface in spherical coordinates is given. Find the equation of the surface in rectangular coordinates. Identify and graph the surface.
[T] ![]()
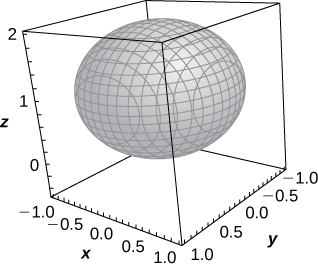
Sphere of equation ![]() centered at the origin with radius
centered at the origin with radius ![]()
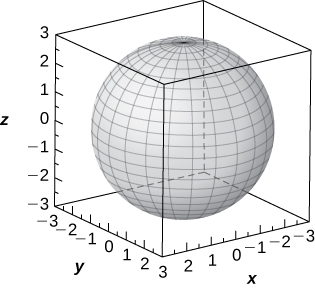
[T] ![]()
[T] ![]()
Sphere of equation ![]() centered at
centered at ![]() with radius
with radius ![]()
[T] ![]()
[T] ![]()
The xy-plane of equation ![]()
[T] ![]()
For the post-obit exercises, the equation of a surface in rectangular coordinates is given. Detect the equation of the surface in spherical coordinates. Identify the surface.
![]()
![]()
For the following exercises, the cylindrical coordinates of a betoken are given. Find its associated spherical coordinates, with the mensurate of the angle ![]() in radians rounded to iv decimal places.
in radians rounded to iv decimal places.
[T] ![]()
![]()
[T] ![]()
![]()
![]()
![]()
For the following exercises, the spherical coordinates of a point are given. Find its associated cylindrical coordinates.
![]()
![]()
![]()
![]()
![]()
![]()
For the following exercises, find the most suitable organization of coordinates to describe the solids.
The solid situated in the first octant with a vertex at the origin and enclosed by a cube of edge length ![]() where
where ![]()
Cartesian system, ![]()
A solid inside sphere ![]() and outside cylinder
and outside cylinder ![]()
Cylindrical system, ![]()
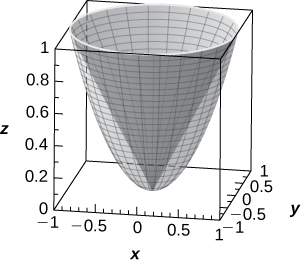
[T] Employ a CAS to graph in cylindrical coordinates the region between elliptic paraboloid ![]() and cone
and cone ![]()
The region is described past the set of points ![]()
[T] Utilise a CAS to graph in spherical coordinates the "ice foam-cone region" situated above the xy-plane between sphere ![]() and elliptical cone
and elliptical cone ![]()
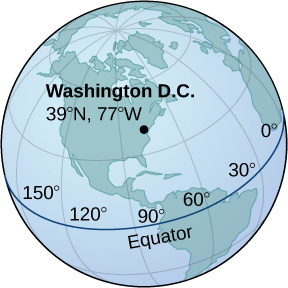
Washington, DC, is located at ![]() N and
N and ![]() Westward (see the post-obit figure). Assume the radius of Earth is
Westward (see the post-obit figure). Assume the radius of Earth is ![]() mi. Express the location of Washington, DC, in spherical coordinates.
mi. Express the location of Washington, DC, in spherical coordinates.
![]()
Notice the latitude and longitude of Rio de Janeiro if its spherical coordinates are ![]()
![]()
![]()
Detect the latitude and longitude of Berlin if its spherical coordinates are ![]()
Chapter Review Exercises
For the post-obit exercises, decide whether the statement is true or false. Justify the answer with a proof or a counterexample.
For vectors ![]() and
and ![]() and whatever given scalar
and whatever given scalar ![]()
![]()
Truthful
The symmetric equation for the line of intersection between two planes ![]() and
and ![]() is given past
is given past ![]()
False
For the following exercises, utilize the given vectors to observe the quantities.
Find the values of ![]() such that vectors
such that vectors ![]() and
and ![]() are orthogonal.
are orthogonal.
![]()
For the following exercises, find the unit vectors.
Find the unit vector that has the same direction as vector ![]() that begins at
that begins at ![]() and ends at
and ends at ![]()
![]()
For the following exercises, find the expanse or volume of the given shapes.
The parallelogram spanned by vectors ![]()
The parallelepiped formed past ![]() and
and ![]()
![]()
For the following exercises, find the vector and parametric equations of the line with the given properties.
The line that passes through point ![]() that is parallel to vector
that is parallel to vector ![]()
The line that passes through points ![]() and
and ![]()
![]()
For the following exercises, find the equation of the plane with the given properties.
The plane that passes through point ![]() and has normal vector
and has normal vector ![]()
The plane that passes through points ![]()
![]()
For the following exercises, detect the traces for the surfaces in planes ![]() Then, depict and draw the surfaces.
Then, depict and draw the surfaces.
![]()
![]()
For the following exercises, write the given equation in cylindrical coordinates and spherical coordinates.
![]()
For the post-obit exercises, convert the given equations from cylindrical or spherical coordinates to rectangular coordinates. Identify the given surface.
![]()
![]()
![]() sphere
sphere
For the post-obit exercises, consider a small boat crossing a river.
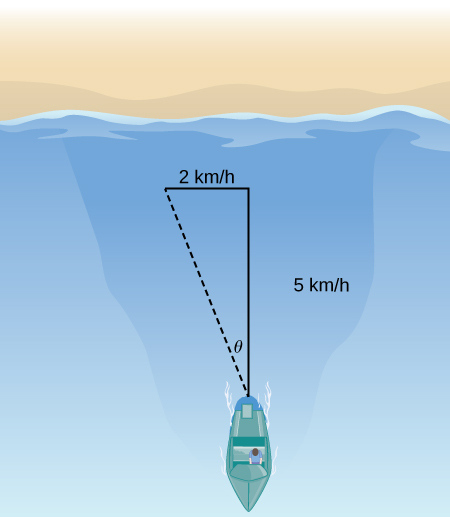
If the boat velocity is ![]() km/h due n in even so water and the water has a electric current of
km/h due n in even so water and the water has a electric current of ![]() km/h due west (encounter the following effigy), what is the velocity of the boat relative to shore? What is the angle
km/h due west (encounter the following effigy), what is the velocity of the boat relative to shore? What is the angle ![]() that the gunkhole is actually traveling?
that the gunkhole is actually traveling?
When the gunkhole reaches the shore, two ropes are thrown to people to help pull the boat ashore. I rope is at an angle of ![]() and the other is at
and the other is at ![]() If the gunkhole must be pulled straight and at a force of
If the gunkhole must be pulled straight and at a force of ![]() discover the magnitude of force for each rope (see the following effigy).
discover the magnitude of force for each rope (see the following effigy).
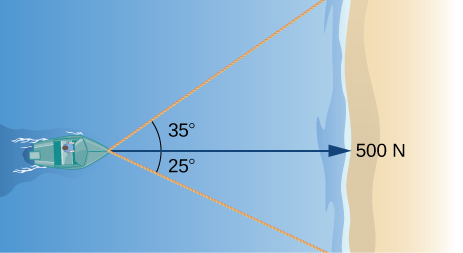
331 N, and 244 N
An airplane is flight in the direction of 52° east of north with a speed of 450 mph. A strong wind has a bearing 33° e of north with a speed of fifty mph. What is the resultant basis speed and bearing of the plane?
Calculate the work done by moving a particle from position ![]() to
to ![]() along a straight line with a force
along a straight line with a force ![]()
![]()
The following issues consider your unsuccessful attempt to take the tire off your car using a wrench to loosen the bolts. Assume the wrench is ![]() m long and you are able to apply a 200-N strength.
m long and you are able to apply a 200-N strength.
Considering your tire is flat, you are only able to utilise your strength at a ![]() angle. What is the torque at the centre of the commodities? Presume this force is not enough to loosen the bolt.
angle. What is the torque at the centre of the commodities? Presume this force is not enough to loosen the bolt.
Someone lends you a tire jack and you are now able to apply a 200-Northward force at an ![]() angle. Is your resulting torque going to exist more or less? What is the new resulting torque at the eye of the bolt? Assume this force is not enough to loosen the bolt.
angle. Is your resulting torque going to exist more or less? What is the new resulting torque at the eye of the bolt? Assume this force is not enough to loosen the bolt.
More than, ![]() J
J
campbellantom1966.blogspot.com
Source: https://opentextbc.ca/calculusv3openstax/chapter/cylindrical-and-spherical-coordinates/
0 Response to "Projection of Sphere Onto Xy Plane How to Draw"
Enregistrer un commentaire